Finding mod(power(x,y)) for Larger Values

The following piece of Pl/SQL uses a clever bit of math to be able to raise a number to a very large power without having overflow problems.

Suppose, for example, you wanted to calculate 2³¹⁸ % 367 (2 to the 318th power, mod 367).

SQL ought to be able to handle this computation, since the answer will only be between 0 and 366 inclusive.

But it runs into issues when we try to raise 2 to the 318th power:

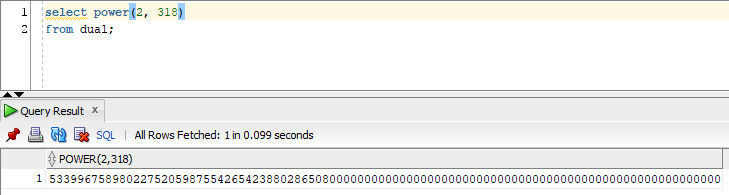
Oracle is unable to handle really, really large numbers with precision, so we get a bunch of trailing zeros at the end of our number.

So if we try to wrap this in a mod function like so:

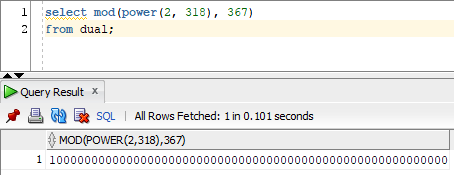
Well, clearly we get the wrong answer since we know the answer couldn’t possibly be more than 366.

I wrote a Pl/SQL function that is able to handle larger numbers efficiently and give us an accurate answer by taking advantage of some clever discrete math. Here it is:

create or replace function power_mod (p_base in number, p_exp in number, p_mod in number)
  return number
  authid definer 
  deterministic 
  parallel_enable
is
  v_bit_index pls_integer := 1;
  type t_bit_array is table of number index by pls_integer;
  v_bit_array t_bit_array;

  v_value number;
  v_max_bit pls_integer;

  v_answer number := 1;
  v_log_base_2 number;
begin

  v_log_base_2 := ceil(log(2, p_exp));

  v_value := mod(p_base, p_mod);
  v_bit_array(v_bit_index) := v_value;
  

  loop
    v_bit_index := v_bit_index + 1;
    v_value := mod(v_value * v_value, p_mod);
    v_bit_array(v_bit_index) := v_value;

    exit when v_bit_index > v_log_base_2;
  end loop;

  -- Here, max bit should equal ceil(log(2, p_exp)) + 1,
  -- which is the maximum number of bits needed to represent a number.
  v_max_bit := v_bit_index;

  for v_index in 1 .. v_max_bit loop    

    if bitand(p_exp, power(2, v_index - 1 )) <> 0 then
      v_answer := mod(v_answer * v_bit_array(v_index), p_mod);
    end if;

  end loop;
 
  return v_answer;
end power_mod;
/

How it Works

It works by taking advantage of an additive property of exponents when like coefficients are multiplied.

So if you have n¹⁵, that’s the same as, say, n⁷ x n⁸. (because 7 + 8 = 15)

We can also “spell out” n¹⁵ in a binary representation using powers of two.

n¹ x n² x n⁴ x n⁸ = n¹⁵

And actually, you can do this with any number. For example, 5

n¹ x n⁴ = n⁵

Notice we skipped n² because when you write 5 in binary, there is not a 1 in the “2’s place,” but there is a 1 in the 1s place an in the 4s place.

5 in binary = 101

What we can do is take out a large number…say 318, and figure out how many bits we would need to represent 318 as a number.

We do this by taking the ceiling of the log base 2 of 318, and adding 1 to it. (i.e. ceil(log(2, 318)) + 1)

Then we build an associative array of the number, with each slot in the array representing a binary number, each number calculated by squaring the previous number.

E.g. v_bit_array[1] = n1
v_bit_array[2] = n2
v_bit_array[3] = n4
v_bit_array[4] = n8
v_bit_array[5] = n16

etc…

We then “spell out” whatever the exponent is in binary.

So if it’s 318, that’s going to be 0001 0011 1110

Meaning we take the second, third, fifth, sixth, and ninth positions in our associative array, and multiply them together (corresponding with where the 1’s are in our binary number).

Since we’re doing a modulus operation, after each multiplication we do (both, when building the associative array and when multiplying the various array slots) to prevent any kind of overflow.

Back to the Original Problem

So now, if we want to know what 2³¹⁸ % 367 is, we can run our function:

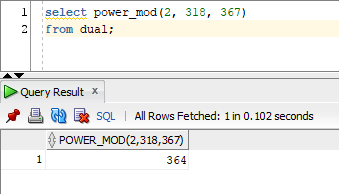
And it gives us the correct answer of 364, no overflow errors.

Free Oracle SQL Tuning Guide

Checkout my FREE guide, 7 SQL Tuning Secrets You Can Use Immediately, Even If You’ve Never Tuned a Query In Your Life!

Get it here: tuningsql.com/secrets